Présentations - 1) Joseph FOURIER /FFT/FFT-1

/ / /

Présentations - 1) Joseph FOURIER /FFT/FFT-1

Le Baron Jean Baptiste Joseph FOURIER

(21 mars 1768 - 16 mai 1830/ 64 ans)

Mathématicien et Physicien Français

uel grand homme ! qui entre autre jeta une partie des bases mathématiques du traitement du signal en proposant ses travaux sur les séries.

Pour la petite histoire, Il fait partie des 72 savants dont le nom est inscrit sur la Tour Eiffel. Un bel article sur Wikipédia lui est consacré.

Vous trouverez en bas de cette page l'Histoire de sa vie, une vie difficile et surprenante, "Orphelin à 8 ans, il sera placé..."

1.1 - Les Transformées : Simple, Rapide, -1, Discrète

Les travaux de Joseph FOURIER ont permis de démontrer qu'un son complexe se divise en plusieurs sons simples.

1.1.1 - Transformée de Fourier / Fourier Transfrom / FT

La Transformée de Fourier (FT) permet la décomposition d'un signal complexe en une multitude de fréquence (décomposition). Elle est très utilisée pour l'analyse Harmonique.

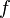La transformée de Fourier $\mathcal{F}$ est une opération qui transforme une fonction intégrable sur $\R$ en une autre fonction, décrivant le spectre fréquentiel de cette dernière : Si $f\$ est une fonction intégrable sur $\R$ , sa transformée de Fourier est la fonction $\mathcal{F}(f)=\hat f$ donnée par la formule :

$\mathcal{F}(f):\xi\mapsto \hat{f}(\xi) = \int_{-\infty}^{+\infty} f(x)\, e^{-i \xi x}\, dx$

1.1.2 - Transformée de Fourier / Fourier Transform ^-1 / FT^-1

La Transformée de Fourier inverse

Si la transformée de Fourier de f est elle-même une fonction intégrable, la formule dite de transformation de Fourier inverse, opération notée $\mathcal{F}^{-1}$ , est celle qui permet (sous conditions appropriées) de retrouver f à partir des données fréquentielles :

$f(x) = {1 \over 2\pi}\, \int_{-\infty}^{+\infty} \hat f(\xi)\, e^{+i\xi x}\, d\xi$ pour $\hat f(\xi)\ = \int_{-\infty}^{+\infty} f(x)\, e^{-i \xi x}\, dx$

Cette opération de transformation de Fourier inverse a des propriétés analogues à la transformation directe, puisque seuls changent le coefficient multiplicatif et le $- i$ devenu $i$ .

Dans le cas des définitions alternatives, la transformée de Fourier inverse devient:

Définition en fréquence:

$f(t) = \int_{-\infty}^{+\infty} \hat f(\nu)\, e^{+i 2\pi\nu t}\, d\nu$ pour $\hat{f}(\nu) = \int_{-\infty}^{+\infty} f(t)\, e^{-i 2\pi\nu t}\, dt$

1.1.3 - Transformée de Fourier Rapide / Fast Fourier Transform / FFT

et Transformée de Fourier Discrète / TFD

Cependant, en traitement du signal, on utilisera la Transformée de Fourier Rapide (FFT).

La transformée de Fourier rapide (sigle anglais : FFT ou Fast Fourier Transform) est un algorythme de calcul de la transformée de Fourier discrète (TFD).

Sa définition mathématique pour un signal $s$ de $N$ échantillons est la suivante :

$S(k) = \sum_{n=0}^{N-1}s(n)\cdot e^{-2 i \pi k \frac{n}{N}} \qquad pour \qquad 0 \leq k < N$

La transformée inverse est donnée par :

$s(n) = \frac{1}{N} \sum_{k=0}^{N-1}S(k)\cdot e^{2 i \pi n \frac{k}{N}}$

On obtient ainsi une représentation spectrale discrète du signal échantillonné $s (n)$ .

Il est important de comprendre que la TFD ne calcule pas le spectre continu d'un signal continu.

La TFD permet seulement d'évaluer une représentation spectrale discrète (spectre échantillonné) d'un signal discret (signal échantillonné) sur une fenêtre de temps finie (échantillonnage borné dans le temps).

1.2.1 Sa vie

Une vie dure mais un être remarquable qui a su se créer un parcours incroyable .

Orphelin à 8 ans

Fils d'un tailleur d'origine lorraine, il devint orphelin à huit ans, fut d'abord recueilli par un maître de pension qui lui donna les premières notions du latin, puis, à la recommandation d'une dame charitable qui avait remarqué ses précoces dispositions, fut placé par l'évêque d'Auxerre à l'école militaire de cette ville, que dirigeaient alors les bénédictins de la congrégation de Saint-Maur.

Découverte des mathématiques à 13 ans

Ce fut un brillant élève. Les mathématiques, qu'il aborda en 1781, le passionnèrent surtout; on le vit renoncer subitement à tous les plaisirs de l'enfance; il se levait même la nuit, content ses biographes, et allait se cacher dans un placard où, à la lueur de bouts de chandelle dérobés un peu partout, il dévorait les livres de Bezout et de Clairaut.

Professeur à seize ans

A seize ans, d'élève il passa professeur. Il aurait bien voulu entrer dans l'artillerie ou dans le génie, et les inspecteurs de l'école firent dans ce but des démarches : le ministre objecta son humble naissance et sa pauvreté. Il se rabattit sur le cloître, se rendit en 1787 à l'abbaye de Saint-Benoît-sur-Loire pour y faire son noviciat de bénédictin, mais, sous l'influence des événements politiques, quitta deux ans après l'habit religieux et revint à son ancienne école où, à l'enseignement un instant délaissé des mathématiques, il joignit celui de la rhétorique, voire de l'histoire et de la philosophie (1789-93).

Présentation à l'Académie des sciences

Entre temps (fin 1789), il était allé présenter à l'Académie des sciences de Paris son premier mémoire, écrit en 1787, « sur la résolution des équations numériques de degré quelconque ».

Il participe à la Révolution Française

Dès la formation des fameux comités de surveillance (avril 1793), il fut élu membre de celui d'Auxerre; admirateur enthousiaste de la Révolution, il ne remplit toutefois ses terribles fonctions qu'avec modération et arracha plus d'un suspect à l'échafaud, entre autres la mère du futur maréchal Davout. Lui-même fut quelque temps incarcéré sur l'ordre du comité de Salut public (juin 1794); il faillit l'être encore après la réaction du 9 thermidor, cette fois sous la prévention de jacobinisme (mars 1795).

Maître de Conférences à l' Ecole Normale puis à l'Ecole Polytechnique

Lors de la création de l'École normale, le district de Saint-Florentin (Yonne) l'y avait envoyé comme élève (janvier 1795); il y devint presque tout de suite maître de conférences et, après sa fermeture, entra à l'École polytechnique, où il fut d'abord simple surveillant des leçons de fortification, mais où il obtint bientôt une chaire d'analyse (1795-98).

Expédition en Egypte

L'expédition d'Égypte fut l'une des plus importantes étapes de sa vie. Emmené par Monge et nommé, dès l'arrivée, secrétaire perpétuel de l'institut du Caire (août 1798), il déploya une prodigieuse et intelligente activité, organisant des fabriques pour les besoins de l'armée, inventant des machines, se livrant à des recherches de tous genres et remplissant ensuite de ses intéressantes communications les séances de la savante compagnie ou les colonnes des publications locales.

Expéditions scientifiques et Diplomatie en Egypte pour Napoléon Bonaparte

Un peu avant le départ de Bonaparte (août 1799), il fut mis à la tête de l'une des deux expéditions scientifiques envoyées dans la vallée du haut Nil. Il fut ensuite chargé de fonctions administratives et diplomatiques des plus délicates : chef de l'administration de la justice, commissaire auprès du divan égyptien, etc. Très éloquent et très persuasif, il s'en acquitta avec un tact et une habileté rares; ce fut lui, en particulier, qui négocia le traité d'alliance avec Moûrâd Bey (avril 1800). Aux funérailles de Kléber (17 juin 1800), il adressa, dans une émouvante oraison, le suprême adieu de l'armée à l'infortuné général. Quelques mois avant l'évacuation, ses collègues de l'Institut lui confièrent la réunion des matériaux du grand ouvrage sur l'Égypte et la rédaction de son introduction générale.

Nomination en tant que Préfet de l'Isère par Napoléon Bonaparte

A son retour en France (septembre 1801), il sollicita un emploi dans l'instruction publique. Mais Bonaparte le nomma préfet de l'Isère (2 janvier 1802). Sa prudente administration apaisa rapidement les esprits, et, sous son active impulsion, la plupart des services de son département furent améliorés (écoles, chemins vicinaux, etc.), en même temps que d'importants travaux étaient entrepris (dessèchement des vastes marais de Bourgoin [1807-12], qui infectaient une quarantaine de communes; ouverture d'une route de Grenoble à Turin par le mont Genèvre, etc.).

Productions scientifiques (analytiques et thermiques)

Il trouva encore des loisirs pour travailler à la Description de l'Égypte et pour continuer ses recherches scientifiques; c'est même de cette époque que datent ses plus belles productions analytiques et thermiques.

Recoit le titre de Baron puis celui de Comte

En 1808, il avait reçu de l'empereur le titre de baron, avec dotation. La révolution de 1814 ne le gêna pourtant pas autrement : il envoya son adhésion au gouvernement des Bourbons, qui le maintint dans sa préfecture. Le retour de l'île d'Elbe le rendit plus perplexe; il tenta d'organiser à Grenoble une résistance, puis s'enfuit vers Lyon, mais, rejoint et admonesté par Napoléon, fit sa soumission. Il fut, en récompense, promu au titre de comte, que, du reste, il ne porta jamais, et mis à la tête de la préfecture du Rhône (10 mars 1815). Les exigences d'une politique pour laquelle il n'était pas fait l'obligèrent à démissionner au bout de quelques semaines (1^er mai 1815);

Direction du bureau de statistique à Paris

il rentra à Paris, où, naturellement mal accueilli par la nouvelle Restauration, il serait tombé dans le plus grand dénuement si son ancien élève et ami, le comte de Chabrol de Volvic, alors préfet de la Seine, ne lui avait confié la direction du bureau de statistique.

Entrée à l'Académie des sciences et à l'Académie Française, Président du conseil de l'Ecole Polytechnique

Le 27 mai 1816, l'Académie des sciences l'élut à une place de membre libre: Louis XVIII refusa de ratifier. Désigné de nouveau, et à l'unanimité, le 12 mai 1817, pour succéder à Rochon dans la section de physique générale, il obtint, celte fois, l'agrément royal. Il devint ensuite secrétaire perpétuel pour les sciences mathématiques en remplacement de Delambre (novembre 1822), membre de l'Académie française en remplacement de Lemontey (décembre 1826), président du conseil de perfectionnement de l'École polytechnique en remplacement de Laplace (1827), et mourut presque subitement d'une hypertrophie du coeur le 16 mai 1830. La Société royale de Londres et nombre d'autres académies étrangères se l'étaient attaché.

La ville d'Auxerre lui a élevé en 1849 une statue en bronze due à Faillot.

1.3.1 - Ses Travaux

Joseph Fourier a exercé sur le développement de la physique mathématique une influence décisive. Les méthodes analytiques qu'il a dû créer de toutes pièces pour arriver à poser ses lois de la thermodynamique présentent, en effet, un caractère de généralité absolue et trouvèrent par la suite un vaste champ d'applications nouvelles, particulièrement en électricité.

En réalité, c'est bien plus la science dans son universalité abstraite qui a profité de ses découvertes que telle branche sur laquelle ses efforts semblent, de prime abord, avoir spécialement porté, et si le titre de physicien ne peut lui être refusé, au fond et avant tout il a été un grand géomètre. Ses plus mémorables travaux se partagent en deux groupes les uns se rapportant à la théorie de la chaleur, les autres à la résolution des équations numériques.

1.3.1.1 - Théorie Mathématique de la Chaleur

La théorie mathématique de la chaleur fut l'objet de ses recherches dès la fin du XVIII^e siècle. Il en communiqua les premiers résultats à l'Académie des sciences le 21 décembre 1807 dans un mémoire longtemps cru perdu et retrouvé près un siècle plus tard Darboux à la bibliothèque de l'École des ponts et chaussées (ms. n° 267). En 1811, l'Académie proposa comme sujet du grand prix de mathématiques :

« Donner la théorie mathématique des lois de la propagation de la chaleur et comparer le résultat de cette théorie à des expériences exactes.»

Fourier envoya un travail très étendu : Théorie des mouvements de la chaleur dans les corps solides (Mém. de l'Acad. des sc., 2 parties, t. IV et V), qui fut couronné le 6 janvier 1812 et dont la première partie a paru à part sous le titre : Théorie analytique de la chaleur (Paris, 1822, in-4; Breslau, 1883, in-4).

Nous ne pouvons donner ici un aperçu, même sommaire, des richesses contenues dans cette oeuvre capitale, qui a fait époque dans l'histoire des mathématiques et de la physique.

Fourier part de ce principe que tous les phénomènes de propagation dépendent de quatre conditions spécifiques, et il formule, tant pour la surface que pour l'intérieur des corps, des équations différentielles au moyen desquelles, trois des conditions étant connues, la quatrième peut se déduire mathématiquement et sans expériences; il intègre ensuite ces équations.

Des mémoires et des notes du même savant, disséminés dans les Annales de chimie et de physique (t. IV, VI, X, XIII, XXII, XXV II, XXVI I, XXXVII), dans le Bulletin de la Société philomathique (années 1818 et 1820), dans les Mémoires de l'Académie des sciences (t. VII, VIII, XII), et relatifs aux propriétés de la chaleur rayonnante, à la température des habitations, au refroidissement séculaire du globe terrestre, à la température des espaces planétaires, à des expériences thermo-électriques (en commun avec Oersted), au mouvement de la chaleur dans les fluides, etc., sont venus compléter et vérifier sa théorie.

1.3.1.2 - Résolution des équations numériques de degré quelconque

Quant à la résolution des équations numériques de degré quelconque,

il avait, nous l'avons vu, écrit dès 1787 et présenté à l'Académie des sciences dès 1789 son premier mémoire sur la question. Il la reprit en 1796 et 1797 dans ses cours d'analyse à l'École polytechnique (les cahiers mss. en sont conservés à la bibl. de l'École des ponts et chaussées), y travailla encore en Égypte (mémoires sur la Résolution générale des équations algébriques, sur les Méthodes d'élimination, etc., dans la Décade égyptienne de l'an VI et de l'an VII), puis à Grenoble, et publia en 1820, dans le Bulletin de la Société philomathique, une note du plus haut intérêt: Sur l'Usage du théorème de Descartes dans la recherche des limites des racines.

La méthode de séparation des racines qui s'y trouve exposée, et qui a donné naissance au beau théorème de Sturm, marque un progrès considérable sur celle de Lagrange; Arago en a contesté la priorité à Fourier en faveur de Budan de Bois-Laurent, mais Darboux a indiscutablement établi que le mérite en revenait tout entier au premier, dont la démonstration s'applique, du reste, aux équations transcendantes, au lieu d'être purement algébrique comme celle de Budan (Mém. de l'Acad. des sc., 1831, t. X). Fourier n'a pas eu le temps de terminer ces recherches, devenues fécondes entre les mains de ses successeurs, et son Analyse des équations déterminées, que Navier a fait paraître d'après ses notes après sa mort (Paris, 1834, in-4), est un ouvrage inachevé. Au même ordre de travaux se rattachent quelques vues nouvelles qu'il a émises sur la théorie des inégalités (Bullet. de la Soc. philom., 1836, et Hist. de l'Acad. des sc. pour 1823 et 1824). (Léon Sagnet).

Applications physiques de la transformée de Fourier

(film de 1966,source Canal U / WebTV de l'enseignement suppérieur)

Applications physiques de la transformée de Fourier :

Partager cette page

Repost0

Le blog de outilsrecherche